在極限問題中會出現(xiàn)與排列組合相結(jié)合的變型考點,這一類題并不難,最主要的還是我們在遇到這樣的題目的時候,反應(yīng)不過來,想不到要用到排列組合。這才是問題的關(guān)鍵所在。
接下來通過一些題目來感受一下這一類型的題目的特點與解題方法。
例 1.箱子里有大小相同的3種顏色玻璃珠各若干顆,每次從中摸出3顆為一組,問至少摸出多少組,才能保證有8組玻璃珠的顏色組合是一樣的?
A.71 B.72 C.73 D.74
答案【A】解析:首先從3種顏色的玻璃球種選出3個,題干中明顯說的是組合數(shù),組合是沒有順序之分的,可以分類為:①3顆玻璃球的顏色一樣,相當(dāng)于從3種顏色中選出1種,有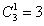 種選法;②3顆球包含2種顏色一定有2顆顏色是一樣的,有
種選法;②3顆球包含2種顏色一定有2顆顏色是一樣的,有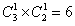 種選法;③3顆玻璃球包含3種顏色,有
種選法;③3顆玻璃球包含3種顏色,有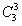 種選法,分類用加法,總共有3+6+1=10種不同顏色的組合,要想保證有8組玻璃球的顏色是一樣的,最不利的情況就是每一種顏色的組合都有7組,這個時候隨便再選一組一定會有8組玻璃球的顏色是一樣的,所求為7×10+1=71,故答案選A。
種選法,分類用加法,總共有3+6+1=10種不同顏色的組合,要想保證有8組玻璃球的顏色是一樣的,最不利的情況就是每一種顏色的組合都有7組,這個時候隨便再選一組一定會有8組玻璃球的顏色是一樣的,所求為7×10+1=71,故答案選A。
方法二:不管從3種顏色中選出3個有多少種選法,一定是個整數(shù),即假設(shè)有n種選法,要求的是需要有8組玻璃球的顏色是一樣的,最不利的情況就是每一種顏色的組合都有7組顏色一樣的,根據(jù)答案=最不利的情況+1,可以得到答案應(yīng)滿足7n+1,即減1能夠被7整除,只有A選項符合。
例 2.某單位組織黨員參加黨史、黨風(fēng)康政建設(shè)、科學(xué)發(fā)展觀和業(yè)務(wù)能力四項培訓(xùn),要求每名黨員參加且只參加其中的兩項。無論如何安排,都有至少5名黨員參加的培訓(xùn)完全相同。問該單位至少有多少名黨員( )。
A.17 B.21 C.25 D.29
答案【C】解析:從4項培訓(xùn)中選出兩項共有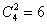 種選法,考慮最不利情況,每種都只有4個黨員參加,則至少需要有
種選法,考慮最不利情況,每種都只有4個黨員參加,則至少需要有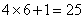 人才能保證有5名黨員所選的培訓(xùn)完全相同。
人才能保證有5名黨員所選的培訓(xùn)完全相同。
例 3.某個社區(qū)老年協(xié)會的會員都在象棋、圍棋、太極拳、交誼舞和樂器五個興趣班中報名了至少一項。如果要在老年協(xié)會中隨機抽取會員進行調(diào)查,至少需要多少個樣本才能保證樣本中有4名會員報的興趣班完全相同?( )
A.93 B.94 C.96 D.97

例 4.某區(qū)要從10位候選人中投票選舉人大代表,現(xiàn)規(guī)定每位選舉人必須從這10中任選兩位投票。問至少有多少位選舉人參加投票,才能保證有不少于10位選舉人投了相同的兩位候選人的票?( )
A.382位 B.406位 C.451位 D.516位
答案【B】解析:從10位里面選出兩位共有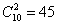 種選舉方式,要保證有10位選舉人投了相同的票,考慮最不利的情況就是每一種選舉方式都有9票,這時只需再加1票就能達到10票相同,共需
種選舉方式,要保證有10位選舉人投了相同的票,考慮最不利的情況就是每一種選舉方式都有9票,這時只需再加1票就能達到10票相同,共需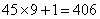 票,答案選B。
票,答案選B。
例 5.調(diào)研人員在一次市場調(diào)查活動中收回了435份調(diào)查問卷,其中80%的調(diào)查問卷上填寫了被調(diào)查者的手機號碼。那么調(diào)研人員至少需要從這些調(diào)查問卷中隨機抽多少份,才能保證一定能找到兩個手機號碼后兩位相同兩個手機號碼后兩位相同的被調(diào)查者?
A.101 B.175 C.188 D.200
答案【C】解析:分兩步考慮最不利原則。首先抽取的恰好全部是20%未填手機號碼的問卷,共有435×20%=87份;接著再次抽取的手機號碼后兩位全不同,每一位上的數(shù)字都有10種情況(0-9),根據(jù)分步原理后兩位總共有10×10=100種情況,故至少需抽出87+100+1=188份問卷才能保證有兩個手機號碼后兩位相同。答案選C。
例 6.某工廠有100名工人報名參加了4項專業(yè)技能課程中的一項或多項,已知A課程與B課程不能同時報名。如果按照報名參加的課程對工人進行分組,將報名參加的課程完全一樣的工人分到同一組中,則人數(shù)最多的組最少有多少人?
A.7 B.8 C.9 D.10
答案【D】解析:排列組合結(jié)合最值問題。要從4項專業(yè)技能課程中選出1項或多項,且A和B不能同時報名,可以分類為:①選擇1門課程,有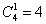 選法;②選擇2門課程,可以用總的情況減去A和B同時報名的情況,有
選法;②選擇2門課程,可以用總的情況減去A和B同時報名的情況,有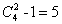 種選法;③選擇3門課程,只能是A或B課程和剩下的2門課程一起選,有2種選法,總共為4+5+2=11種報名方式。將所有報名方式完全一樣的人分到同一組中,要想人數(shù)最多的組人盡可能少,根據(jù)逆向思維,則要讓其他組的人數(shù)盡可能多,即盡可能接近,則可以采取平均分的原則,100÷11=9……1,剩下來的這一個人,隨便分到哪一組中去,都符合條件,所以人數(shù)最多的組最少有10個人。 答案選D。
種選法;③選擇3門課程,只能是A或B課程和剩下的2門課程一起選,有2種選法,總共為4+5+2=11種報名方式。將所有報名方式完全一樣的人分到同一組中,要想人數(shù)最多的組人盡可能少,根據(jù)逆向思維,則要讓其他組的人數(shù)盡可能多,即盡可能接近,則可以采取平均分的原則,100÷11=9……1,剩下來的這一個人,隨便分到哪一組中去,都符合條件,所以人數(shù)最多的組最少有10個人。 答案選D。
雖然這樣的一些題目都需要用的排列組合,但是這樣的排列組合都是比較簡單的一些問題,如果把它們單獨地放到排列組合題中,這個時候排列組合問題的題型特征比較明顯,問的都是有多少種選法,當(dāng)這兩種題型結(jié)合到一起的話,它的難度大大提升了,因為它最終的提問方式為最不利原則的特征,都是“至少……才能保證……”的形式,就會導(dǎo)致這樣的一些題目根本無從下手。
但是通過以上幾個題目,我們也不難發(fā)現(xiàn)它們都有一個共同的特征,就是都涉及到元素的選取問題,排列組合也是一樣的,所以如果這一類題要出得難一點的話,就會結(jié)合一起考察。
相信通過以上幾個題目的話,我們同學(xué)對于這一類題目也有了一定的了解。遇到這樣的問題我們可以將其拆分為兩步去做,先把它當(dāng)成一個排列組合來做,然后再用最不利原則的解題方法就可以啦。


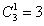
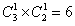
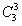
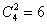
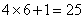

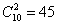
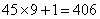 票,
票,